ChineseChess 程序:Minimax 算法与 Alpha-Beta 剪枝
最近用 AI 辅助构建了一个中国象棋人机对战程序,前端界面基于 Web,后端算法用 C++ 实现,目前完成了一个初版。该程序使用的是博弈程序中基本但重要的 minimax 算法,并采用了 Alpha-Beta 剪枝优化,在 4 层的搜索深度下基本上可以达到一个纯象棋初学者的水平。
问题抽象:博弈树
象棋是一种完全知识博弈,任意时刻双方都知道棋盘上的所有状态(扑克、麻将则不是)。随着双方走子,棋盘状态会不断变化。从某一棋局状态开始,棋局演化的可能性可以抽象成一棵以初始状态为根节点的树,称之为“博弈树”。
另外,象棋是一种涉及两方的零和博弈 [2],即任何局面下,双方的获益之和都为 0。在这种游戏中,某一方的获益等价于另一方的损失。举个例子,若某局面下一方的获益是 x,则另一方的获益就是 -x,也可以说此时另一方的损失是 x。为了描述方便,我们可以只使用“获益”的概念。博弈树上的每一个节点对应一个棋局状态,都可以计算相应的获益值,可称之为“得分”。于是,针对当前行棋的一方,我们得到一棵带节点得分的博弈树,如下所示。
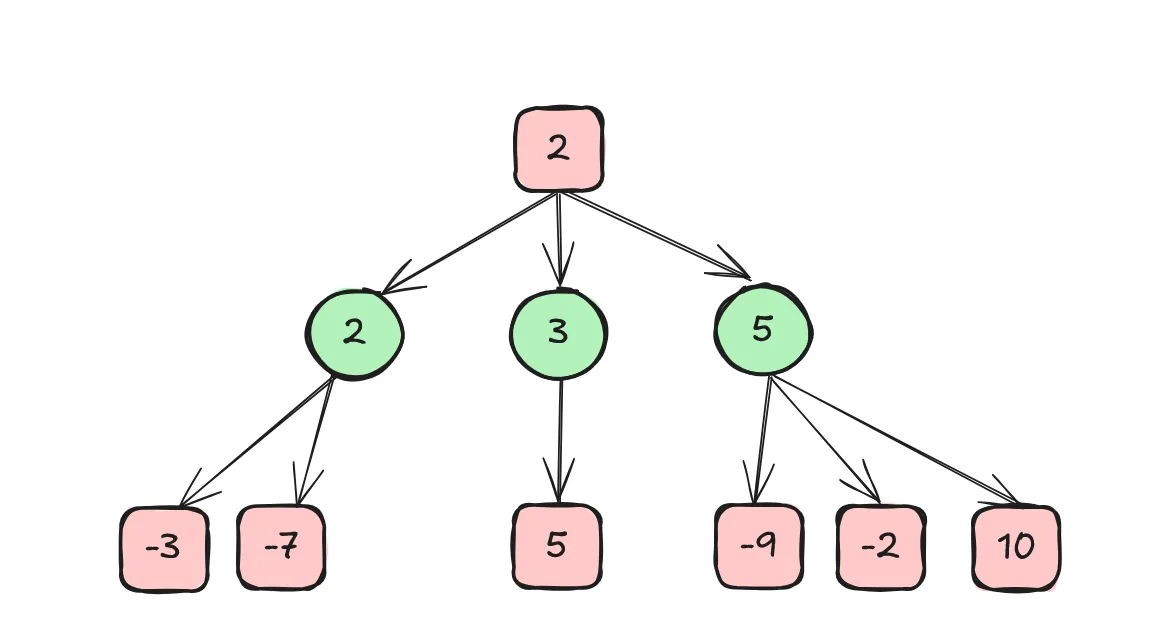
理想情况下,博弈树的叶子节点应该是一个胜负已分的棋局状态,但由于象棋变化众多,目前要生成一棵完整的带全部棋局终态的博弈树是不可能的。假设每个棋局状态有 40 种后续演化,双方各走 50 步,树节点数量就多到 40100。因此,相对于完整的博弈树,我们往往只能构建一棵深度相当有限的树。
现在我们已经将棋局演化的可能性抽象为了博弈树,接下来要做的就是基于博弈树寻找最佳的下一步走法。
Minimax 算法
计算机需要通过对博弈树展开搜索来寻找最佳的下一步走法,在这种博弈环境下寻找最优走法的搜索就是“对抗搜索”,minimax 算法则是对抗搜索中最基本的算法之一。我们一点点来,看看是如何设计出 minimax 算法的。
假设当前是我方走子,我要算棋,算 N 步。对方和我旗鼓相当,我能想到的对方也能想到。
如果我的头脑只能算一步,没什么好说的,直接选我方获益最大的局面就好,即选下图中第三种走法。
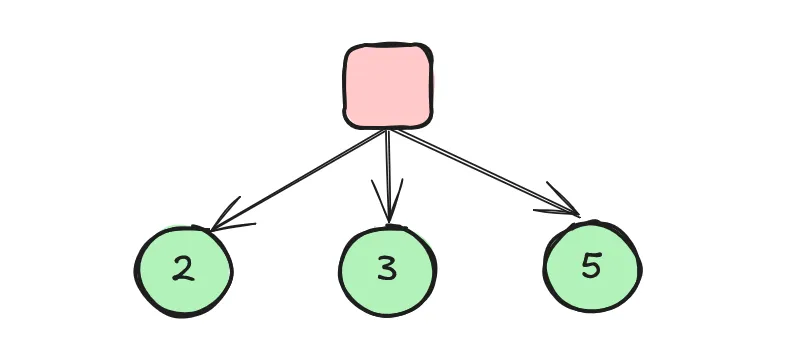
如果我能算两步棋,我要考虑对方会怎么下。既然我的脑子只能算两步棋,那我当然只能帮对方算一步棋了。因此,我预测对方会直接选择对我方最不利的局面。对于当前的三种可选走法,对方会分别使我的获益成为 -7、5、-9。所以我不能选择第三种走法,而要选择第二种。也就是说,我选择了控制风险,让对我方最差的局面也尽可能好。
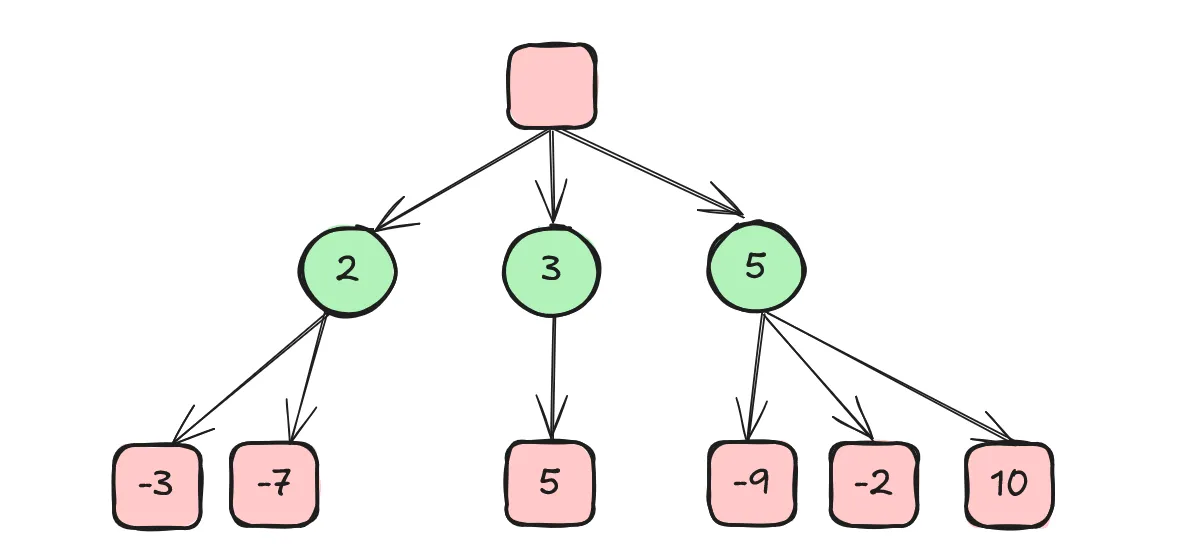
接下来考虑能算三步棋的情况。当我在脑子里下一步棋之后,还要帮对方想两步棋。对方能算两步的话,他会怎么走?他很聪明,不会随意乱下,也会用和我在算两步棋的时候用的一样的套路,即选择对他最差局面最好的走法。如果我选第一种走法,他会选对应情形下的第一种走法,最终我方获益是 8;如果我选第二种,他没得选,最终我方获益是 4;如果我选第三种,他会选对应情形下的第一种走法,最终我方获益是 5。因此,我要选择第一种走法。
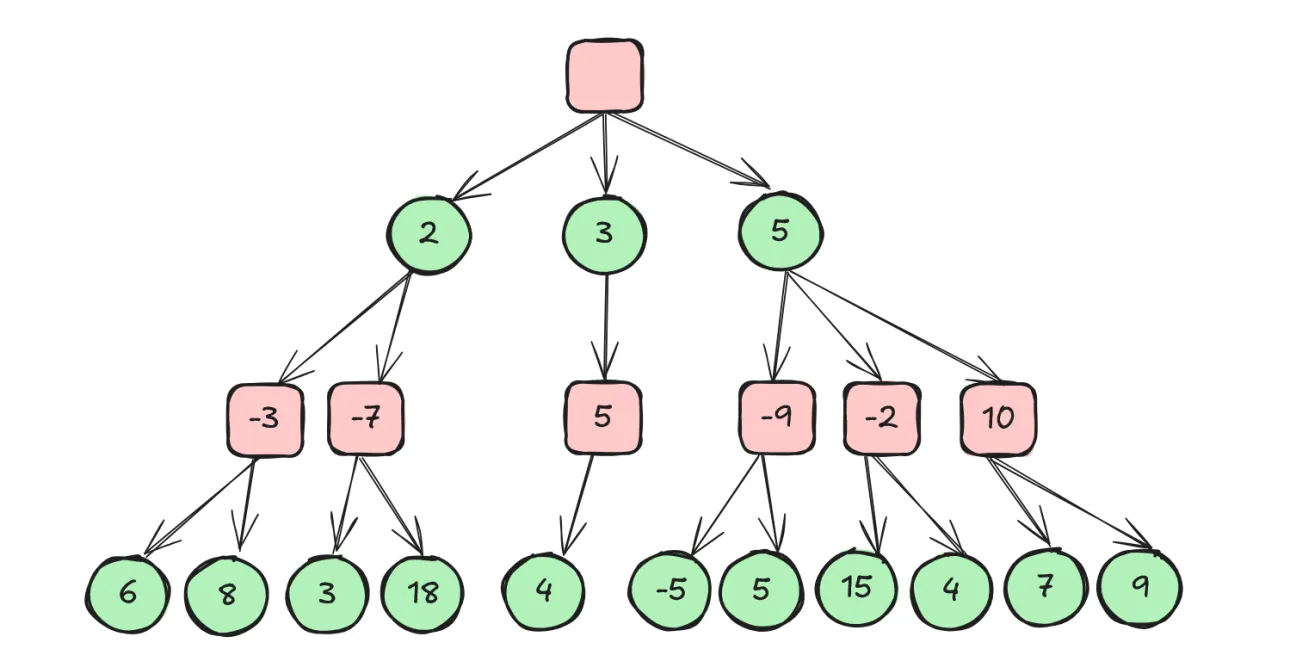
那如果我能算四步呢?同样地,我在脑子里下一步棋之后,还要帮对方想三步棋。预测对方走法时依然假定对方和我使用一样的策略。对于我方可能的每一种走法,都能得到一个最终的局面和对应的分数,从中选出分数最高的最终局面即可。
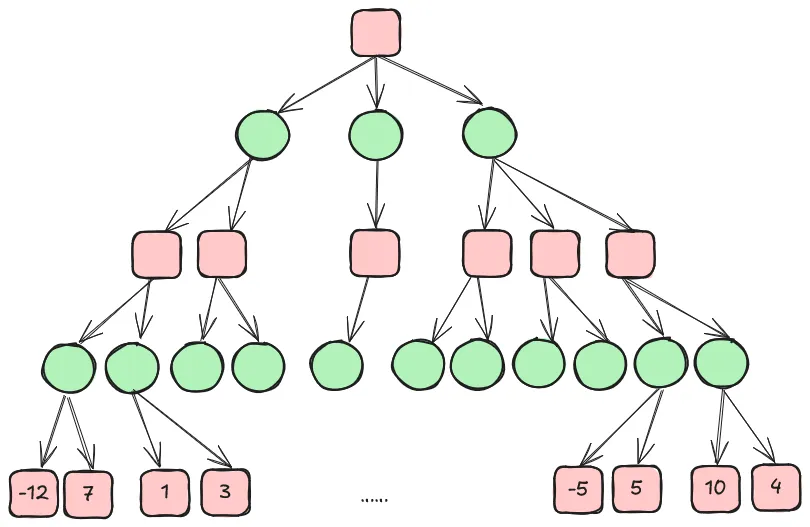
到这里,我们已经可以发现“算棋”其实是一个递归求解的过程。对于当前每一种可能走法,都对应一个子问题,即对方拿着后续的棋局状态去算 N-1 步棋。我们求解子问题时需要拿到最终局面下我方的分数,然后选择返回最大分数的子问题对应的走法。 求解过程可以用代码描述如下:
// 返回最佳走法和最终局面下的我方得分(获益)
func getBestMove(board Board, player Player) (Move, int) {
// 边界情况
if depth == 0 {
return nil, evaluate(board, player)
}
moves := getPossibleMoves()
maxScore := MIN_INT
bestMove := nil
for _, m := range moves {
board.applyMove(m)
// 返回对方的最佳走法和最终局面下的对方得分
_, scoreForOpponent := getBestMove(board, opponent(player))
score := -scoreForOpponent // 对方得分与我方得分是相反数
if score > maxScore {
maxScore = score
bestMove = m
}
board.revertMove(m)
}
return bestMove, maxScore
}那么,该算法为什么叫做 minimax 算法?在“我方预测 N 步棋并找最佳走法”这个问题中,包含“对方预测 N-1 步棋并找最佳走法”的多个子问题。后者的目标是让最终局面尽可能对我方不利,即我方的获益尽可能小,或者等价地说,损失尽可能大。而我方的策略就是在所有最差的最终局面中选择最好的那一个,即最小化最大的损失,这就是 minimax 的含义。
Alpha-Beta 剪枝
上述的纯 minimax 算法已经可以达到一个象棋新手的水平了,但是搜索的速度还比较慢,在没有过多日志打印开销的情况下,该版本的象棋程序预测 4 步棋大约需要 4~5s,我们还需进一步优化其计算速度。
如果我们将树节点的得分统一表示为我方得分,观察 minimax 算法的求解过程(以下面博弈树为例)不难发现:其核心就是自底向上地将当前节点的分数记为其子节点分数的最大值、最小值、最大值……
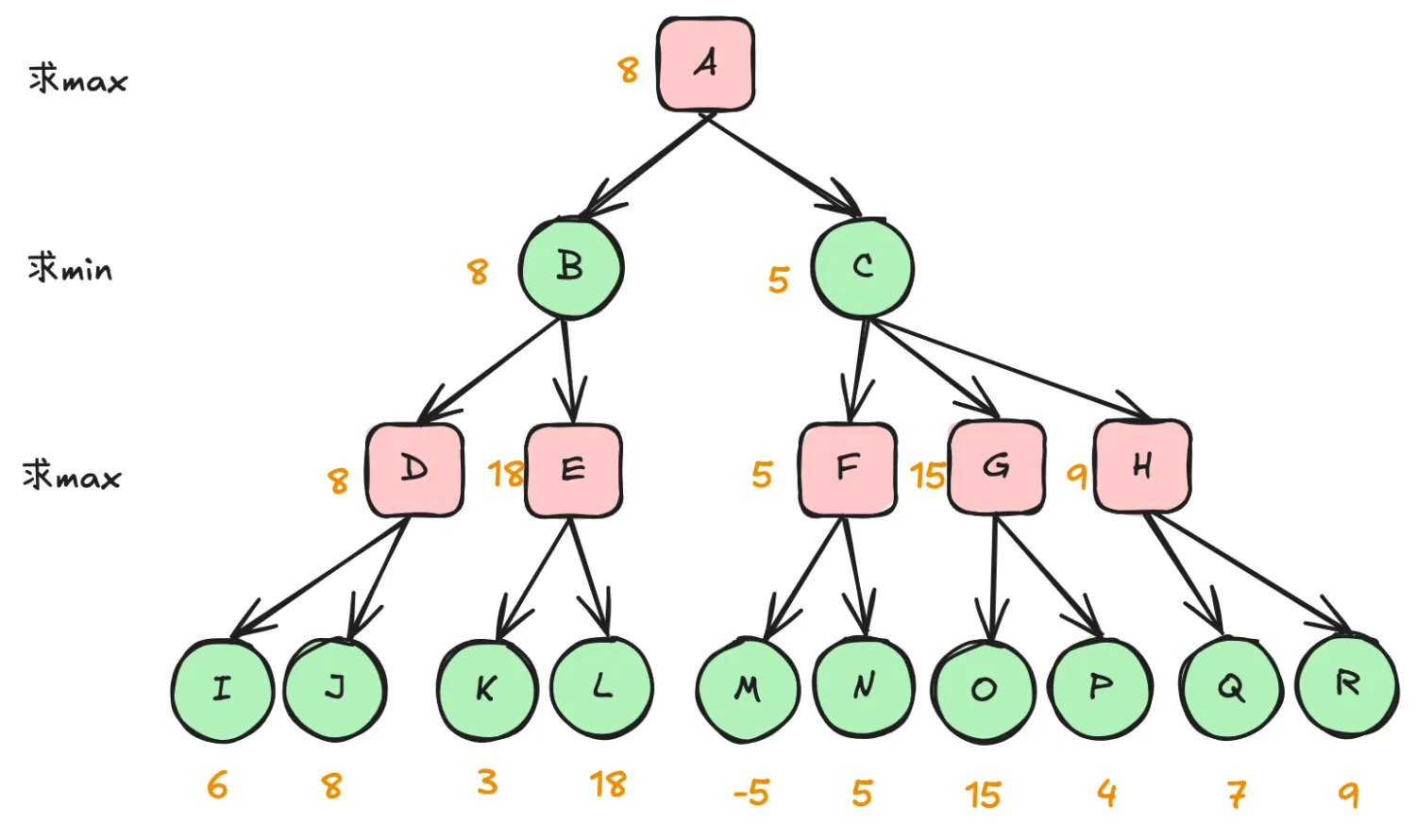
在求解根节点的最佳走法时,假设已经求解出 B 的分数是 8。在求解 C 时,当已经知道 F 的分数为 5 时,C 的后续子节点就无需再求解了。因为第二层是求 min,所以 C 的分数肯定不超过 5,而第一层是求 max,因而肯定不会选择 C。
我们再单独看 C 的求解。假设已经求解出 F 的分数为 5,则当求解 G 并遍历到 O 得知其分数为 15 时,G 的剩余子节点就无需再遍历了。因为第三层是求 max,所以 G 的分数肯定不会低于 15,而第二层是求 min,因而 C 肯定不会选择子节点 G。
上述情况提示我们,在求解子问题时可以给予一定的信息,从而减少子问题中的一部分计算量。在得到 B 的分数后,我们可以在求解 C 时告诉其一个搜索区间 [8, +infinity),只要 C 的子节点已经得出了这个范围之外的分数,则可以立刻终止 C 的求解,并将该分数作为 C 的最终得分,这就是 alpha-beta 剪枝优化。
增加 alpha-beta 剪枝后的 minimax 算法用代码描述如下。注意子问题的搜索区间需要基于当前搜索区间取反,因为子问题中关注的是对方的得分。另外,在顶层调用 getBestMove 函数时要注意不要设置区间 [INT_MIN, INT_MAX],因为 INT_MIN 取反后会发生溢出。
// 返回最佳走法和最终局面下的我方得分(获益)
func getBestMove(board Board, player Player, alpha int, beta int) (Move, int) {
// 边界情况
if depth == 0 {
return nil, evaluate(board, player)
}
moves := getPossibleMoves()
bestMove := nil
for _, m := range moves {
board.applyMove(m)
// 返回对方的最佳走法和最终局面下的对方得分
_, scoreForOpponent := getBestMove(board, opponent(player), -beta, -alpha)
score := -scoreForOpponent // 对方得分与我方得分是相反数
if score > alpha {
alpha = score
bestMove = m
}
if alpha >= beta {
break
}
board.revertMove(m)
}
return bestMove, maxScore
}经验证,在没有 alpha-beta 剪枝的情况下,预测 4 步棋需要约 4~5s,增加剪枝后,只需要约 0.5~1s,粗略估计速度相差 5~10 倍左右。不过,带 alpha-beta 剪枝的版本在预测 5 步棋时也需要大约 4~5s,仍然不能算理想。